Modèle d'équilibre énergétique méridien - EBCM
Application proposée par le Club des Argonautes
Auteur : Yves Fouquart
Codage R-Shiny : Pierre Chevallier
Version : mai 2021
Le système climatique est commandé par les échanges d'énergie qui y ont lieu.
Si l'on considère la planète dans son ensemble , ses échanges d'énergie avec l'extérieur ne se font que par rayonnement. Sur le long terme, ces échanges doivent être équilibrés faute de quoi, la Terre se réchauffe si elle gagne plus d'énergie qu 'elle n'en perd et réciproquement. Actuellement, la Terre perd moins d'énergie qu'elle n'en gagne
La Terre reçoit son énergie du soleil sous forme d'un rayonnement de courtes longueurs d'onde, on appelle irradiance solaire F0 la quantité d'énergie reçue par 1 m2 de surface perpendiculaire à la direction du soleil. La quantité totale reçue par toute la planète par unité de temps est donc F0 S, où S = π R2 est la surface du disque face au soleil avec R, le rayon de la Terre. Elle en réfléchit une partie α vers l'espace ; α est appelé l'albédo de la planète. La quantité d'énergie absorbée est donc π R2 (1-α) F0.
La Terre perd aussi son énergie par rayonnement, mais à des longueurs d'onde plus grandes, dans l'infrarouge. Si on appelle Fir(TOA), la valeur en W/m2 du flux infrarouge sortant au sommet de l'atmosphère, la quantité totale d'énergie perdue par la Terre par seconde est 4π R2 Fir(TOA) et l'équilibre énergétique requiert que
Fir(TOA) = Solabs = (1-α) F0/4
Si l'on s'intéresse, cette fois, aux échanges d'énergie qui ont lieu sur la planète, à l'intérieur du système climatique, il faut faire intervenir les échanges de chaleur qui ont lieu par l'intermédiaire des échanges de matière, c'est à dire par convection et par advection.
Dans cette section, on explore quelques une des principales conséquences qui en résultent. On dispose pour cela de trois modèles
Un modèle d’équilibre énergétique (EBCM : Energy Balance Climate Model) (présenté ici)
Modèle effet de serre
Objectifs : estimations de la sensibilité climatique, du forçage radiatif du CO2, du forçage des nuages, de la rétroaction de la vapeur d'eau.

Deux vidéos de présentation sont disponibles :
La première vidéo se veut abordable pour tous. Elle ne nécessite aucune connaissance préalable, juste un peu d’attention.
La deuxième essaie d’aller un peu plus au fond des choses en introduisant la notion d'altitude d'émission et en présentant les différents modes d'interaction des molécules avec le rayonnement. Elle ne nécessite pas, à vrai dire de connaissances particulières puisque tout y est expliqué mais elle est plus complexe et un peu de familiarité avec la physique permettra évidemment une compréhension plus aisée. On y verra aussi que l’effet de serre est très largement validé par les mesures de température de l’atmosphère qui sont effectuées tous les jours depuis les satellites météorologiques.
Le premier modèle permet d'évaluer l'influence d'une variation de la concentration de gaz à effet de serre (GES) sur la température moyenne à la surface. Les GES qui sont pris en compte sont la vapeur d'eau qui est ajustable par l'intermédiaire de l'humidité relative et le CO2. Le modèle calcule les flux IR à tous les niveaux , entre autres le flux IR sortant au sommet de l'atmosphère, Fir(TOA). On cherche par tâtonnements la température à la surface (*) qui permet de respecter l'équilibre radiatif de la planète :
Fir(TOA) = Solabs = (1-α) F0/4 en W/m²
où : Solabs, énergie solaire absorbée ; α, albédo de la Terre ; F0, irradiance solaire (encore appelée « constante solaire »).
Ce modèle permet en particulier d'évaluer quantitativement l'effet de serre mesuré ici par le rapport entre l'énergie émise par la surface et l'énergie qui sort de l'atmosphère :
G = Fir(z=0) / Fir(sommet de l’atmosphère)
et sa variation quand les concentrations en GES sont modifiées.
L'application calcule les flux infrarouges sortants au sommet de l'atmosphère (TOA : Top of Atmosphere) en fonction de la température de surface, de l'humidité relative, de la concentration en CO2 et de la couverture nuageuse. Pour cette dernière, on considère soit un nuage bas à une altitude comprise entre 1000 et 2000 m d’altitude, soit un nuage haut à une altitude comprise entre 7000 et 8000 m d’altitude.
La méthode consiste à fixer ces paramètres et à chercher par tâtonnements la température de surface qui satisfait l'équilibre énergétique.
L'application calcule aussi le bilan radiatif de l'atmosphère qui est négatif, car celle-ci cède plus d'énergie qu'elle en reçoit. Lorsque l'équilibre est atteint, le bilan radiatif à la surface de la Terre est égal et opposé au bilan de l'atmosphère ce qui correspond au fait que la surface dont le bilan est positif chauffe l'atmosphère par l'intermédiaire des mouvements de convection de l’atmosphère.
Attention:
Cette simulation s'applique à la planète dans son ensemble.
Les calculs sont réalistes, mais très simplifiés , il ne faut donc pas chercher de réponse quantitative comme par exemple, la sensibilité à un doublement de la concentration en CO2 même si la valeur trouvée (2,5 °C) semble raisonnable. La seule rétroaction incluse dans la simulation est celle de la vapeur d'eau : lorsque l'on change la concentration en CO2, la température change elle aussi, et si l'on maintient l'humidité relative constante, la teneur en eau de l'atmosphère varie elle aussi.
Pour une représentation pédagogique avec plus d’options, on peut consulter celle de l’université de Chicago (en anglais) qui ne détaille toutefois pas la méthode utilisée : http://climatemodels.uchicago.edu/rrtm/
Définitions : ici, pour une variation de la concentration en CO2, une rétroaction est la variation de température qui en résulte de façon indirecte comme par exemple :
Augmentation CO2 => augmentation de température => diminution de l'étendue de neige et de glace => diminution de la quantité de rayonnement solaire réfléchi ou de façon équivalente augmentation de la quantité de rayonnement solaire absorbé => augmentation de la température
ou
Augmentation CO2 => augmentation de température => augmentation de la quantité de vapeur d'eau => augmentation de l'effet de serre de la vapeur d'eau => augmentation de la températureou encore
Augmentation CO2 => augmentation de température => augmentation de la végétation => diminution de la concentration en CO2 => diminution de la température
(*) Pour des raisons pratiques de temps de calcul, le modèle est évidemment très simplifié, la température et la pression varient avec l'altitude d'une manière qui correspond à une atmosphère moyenne (la température diminue linéairement avec l'altitude jusque vers 10km et la pression diminue d'environ 100 hPa par km (plus précisément : p = p0 e(-z/H) avec H = 8km) et l'absorption par la vapeur d'eau et le CO2 est calculée d'une façon très approximative. Pour une approche pédagogique, les résultats restent cependant suffisamment proches de ce qui pourrait être obtenu avec des modèles plus précis.
Modèle radiatif convectif (RCM)
Objectifs : répartition de la température avec l'altitude, mise en évidence de la stratosphère, compréhension du mécanisme par lequel l'augmentation de l'effet de serre augmente la température à la surface.
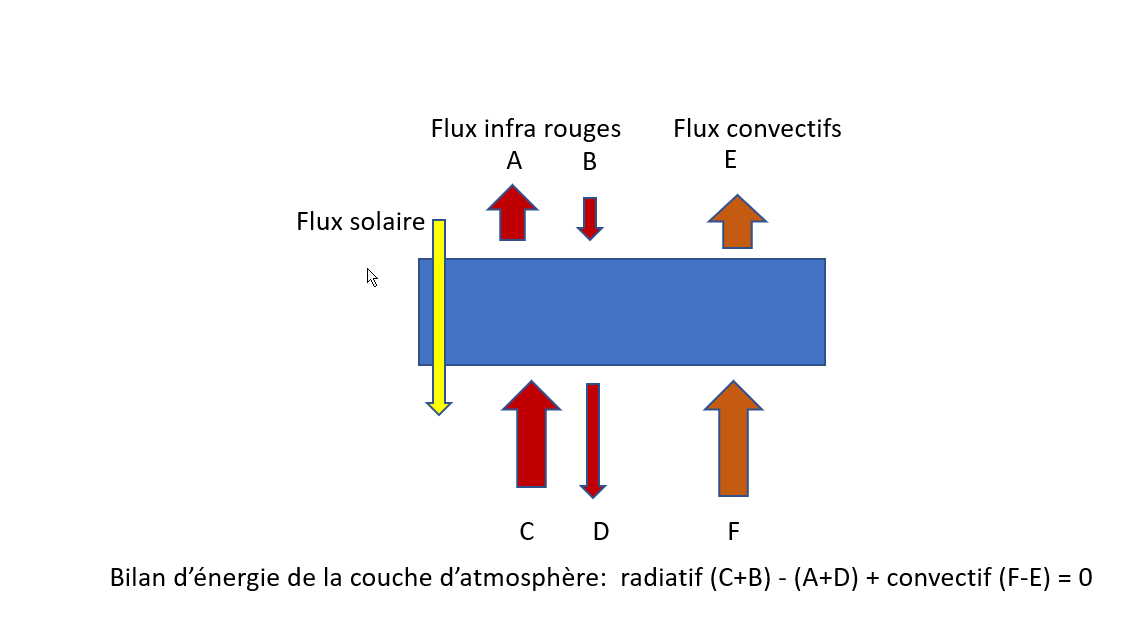
Représentation schématique de l'équilibre radiatif convectif d'une couche d'atmosphère. Ici, l'atmosphère est supposée transparente au rayonnement solaire, c'est une approximation très grossière.
Ce type de modèle a été essentiel dans le développement de la recherche climatique. En 1966 Wetherald et Manabe l'ont développé comme une première étape dans la réalisation du premier modèle tridimensionnel de circulation générale de l’atmosphère qui a donné naissance aux modèles climatiques actuels. Les RCM sont des modèles unidimensionnels (la verticale) dans lesquels la température est le résultat de l'équilibre énergétique entre les apports d'énergie par la convection et par l'absorption du rayonnement solaire et les pertes d'énergie par rayonnement infrarouge. La convection distribue les échanges de chaleur d'une manière telle que la température diminue régulièrement en fonction de l'altitude jusqu'à une certaine altitude (la tropopause) puis, l'énergie convective ayant été entièrement dissipée aux altitudes inférieures, la température reste constante dans la stratosphère.(**)
Les variables sont l'effet de serre dont les limites de variation peuvent être estimées au moyen du premier modèle (modèle d'effet de serre) et l'albédo de la planète(***).
Le modèle permet :
de mettre en évidence l'existence de la stratosphère et d'estimer l'altitude de la tropopause et la façon dont elle varie avec l'effet de serre ou avec la constante solaire ;
d'observer que lorsque l'effet de serre augmente, l'altitude du niveau d'émission du rayonnement qui sort vers l'espace augmente . C'est par cet intermédiaire que l'augmentation la concentration en CO2 provoque l'augmentation de la température à la surface. C'est donc un mécanisme dont la compréhension est essentielle.
(**) Précisions : Dans ce modèle, le gradient de température est fixé à sa valeur moyenne climatique de 6,5°C/km correspondant à une atmosphère standard avec une température à la surface voisine de 15°C. Pour des raisons pratiques de temps de calcul, le modèle est extrêmement simplifié et on ne retient que les paramètres et les processus essentiels qui sont l'absorption et l'émission de rayonnement d'une part et la convection d'autre part. L'absorption du rayonnement solaire par l'atmosphère est négligée. L'absorption par les différents GES est représentée par un coefficient indépendant de la longueur d'onde (on dit que l'absorption est grise). Ce coefficient est directement lié à l'effet de serre.
(***) : Les variations de l'albédo et celles de la constante solaire sont équivalentes. En effet, l'une des hypothèses fondamentales du modèle est l'équilibre radiatif de la planète (eq. 1) et puisque l'atmosphère est transparente au rayonnement solaire, l'albédo de la planète est égal à celui de la surface (l'albédo des nuages est donc combiné à celui de la surface proprement dite).
Modèle d'équilibre énergétique (EBCM: Energy Balance Climate Model)
Objectifs : répartition de la température avec la latitude, estimation des transports de chaleur par l'océan et l'atmosphère, variation avec la température de la surface couverte de glace.
Originellement, le premier EBCM a été développé par Budyko en 1969. Le modèle a une dimension: la latitude.
L'hypothèse est que chaque bande de latitude doit être équilibrée énergétiquement. Ici, le bilan énergétique est la somme du bilan radiatif et du bilan de l'énergie transportée par les mouvements de l'atmosphère et de l'océan, ce qui s'écrit :
Fir(x) = Solabs(x) + Adv(x)
où x est la latitude (****).
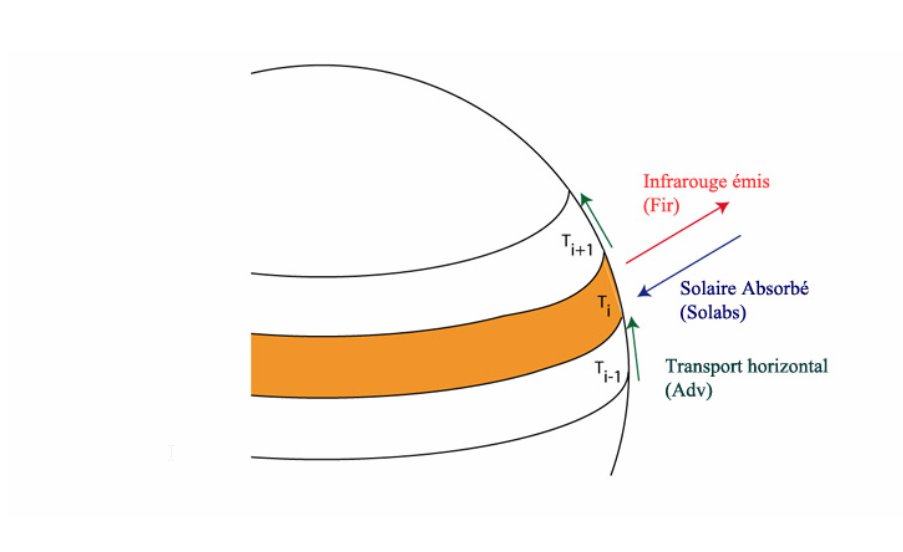
Le modèle calcule le flux infrarouge émis à chaque latitude et par l'intermédiaire de G (la mesure de l'effet de serre), on en déduit la température à la surface.
G = Fsur(x) / Fir(x)
Fsur(x) = σ T(x)4
Le modèle d'effet de serre permet de calculer G en fonction de la concentration en CO2 ou des nuages.
(****) Dans le détail : le flux solaire absorbé dépend de l'ensoleillement à la latitude x et de l'albédo :
Solabs(x) = (1-alb(x)) * ensol(x)
On suppose que le flux advecté, c’est-à-dire que la quantité de chaleur apportée (ou perdue) par les mouvements de l'atmosphère et de l'océan de l'équateur vers les pôles, est proportionnel à la différence entre le flux solaire absorbé en moyenne par la planète (Solmoy) et celui qui est absorbé à la latitude x.
Adv(x) = C * (Solmoy - Solabs(x))
Modèle EBCM
Avertissement : le modèle reste assez grossier ; il ne faut pas en attendre une grande précision, on cherchera plutôt à mieux comprendre comment les choses évoluent quand l'effet de serre varie et on se contentera d'un ordre de grandeur.
Vérification du modèle et calcul des transports méridiens d'énergie
La température moyenne de la planète est voisine de 15°C, l'albédo moyen est lui, voisin de 30%. A partir de l'équilibre radiatif de la Terre , déterminer l'effet de serre G qui satisfait ces conditions.
Indication : σ T4s/G = (1-α) F0/4
Fixer G, faire varier le coefficient d'advection (transport méridien ou en latitude) C (compris entre 0 (pas d'advection) et 1), observer comment varie T(x) (température moyenne zonale).
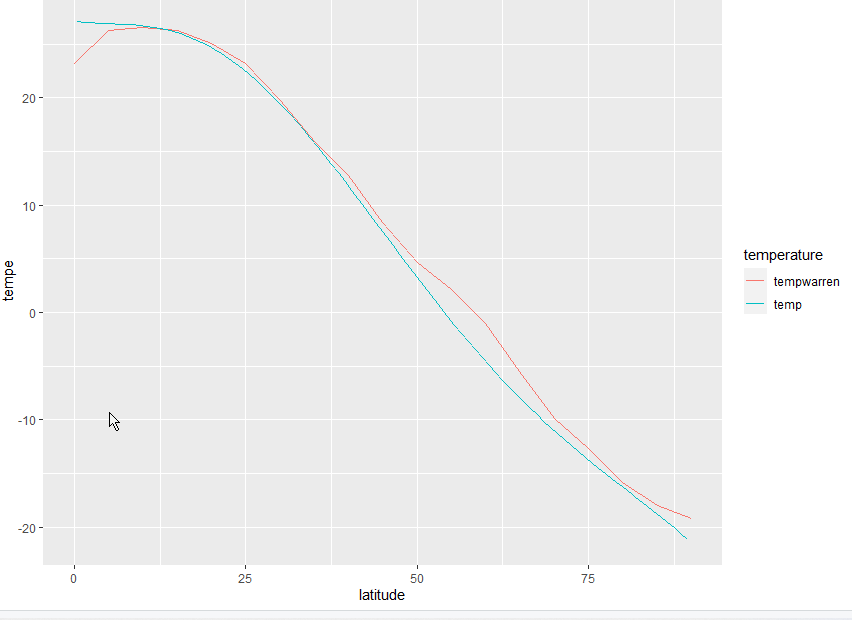
Chercher le meilleur accord entre T(x) et les températures climatologiques (exemple sur la figure ci dessus)
Lorsque G varie, la température moyenne de la planète varie et c'est donc toute la courbe qui est translatée sans grande déformation ; l'advection, c'est-à-dire le transport méridien (en latitude) par l'atmosphère et l'océan, modifie la répartition des températures. Ce transport méridien est présenté sur la partie basse des figures produites par le modèle.
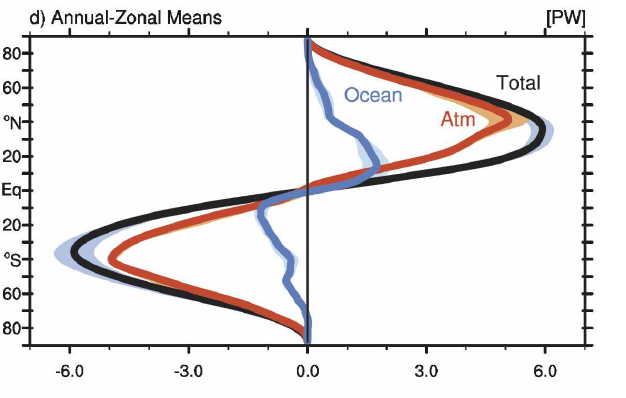
La figure ci dessus (source) est dérivée des mesures du bilan radiatif depuis l'espace ainsi que des réanalyses des observations météorologiques et océaniques , elle présente les transports par l'atmosphère, par l'océan et leur somme.
Rappel : le modèle est symétrique par rapport à l'équateur. Le résultat n'est pas fantastique, le maximum de transport se situe bien vers 30 à 40° de latitude, mais il n'est que d’un peu plus de 4 pétawatts contre près de 6 estimés.
[1 pétawatt = 1015 W ou encore 1 million de GW, c'est à dire l'équivalent de la puissance de 1 million de réacteurs nucléaires du type de celui de Graveline près de Dunkerque].
Evolution de la surface englacée avec l'effet de serre
On utilisera la deuxième option du modèle : albédo « variable », qui ne fixe pas l'albédo en fonction de la latitude mais en fonction de la température. Dans cette version, les paramètres sont l'effet de serre, l'albédo des zones libres de glace toute l'année et l'albédo des zones couvertes de glace ou de neige en permanence. On suppose qu'il n'y a ni neige ni glace si la température annuelle est supérieure à 10°C et qu'au contraire la neige ou la glace sont permanentes si la température est inférieure à -15°C. Entre les deux, l'albédo varie linéairement.
Le coefficient d'advection est fixé à la valeur qui donne le meilleur accord pour la vérification ci-dessus.
A partir du modèle d'effet de serre, calculer G pour la concentration actuelle en CO2 (410 ppm) et pour la concentration préindustrielle (280 ppm). Comparer les superficies englacées
Glaciaire / interglaciaire : Faire de même pour 180 ppm de CO2 correspondant à la concentration du dernier maximum glaciaire, il y a 20 000 ans.
Note : le modèle ne permet pas de séparer océan et continents ; seules les superficies peuvent être comparées à des observations.